05.Grammatiche Formali

Grammatiche Formali

Le grammatiche formali sono un insieme di regole. Hanno 2 alfabeti, un assioma (o simbolo iniziale) e un insieme di regole dette produzioni sintattiche.

Relazione di derivazione

Produzione sintattica che produce da una stringa un’altra. Posso anche eseguirle in sequenza ottenendo quindi un linguaggio. Da L(G) ottengono il linguaggio L1.

Ci sono 4 tipi di grammatiche:

(stringa a è di partenza, stringa b è di arrivo a→b)

• Tipo 0 = nessuna limitazione
• Tipo 1 = |a|<|b|
• Tipo 2 = |a| = 1 (Context Free)
• Tipo 3 = regolari

Regole delle Grammatiche Regolari:

• |a| = 1
• b $\in V_t.V_n\cup V_t$ (nota che $.$ intende la concatenzazione di stringhe)
• b = $ϵ$ sono nel caso in cui la stringa vuota è presente nel linguaggio

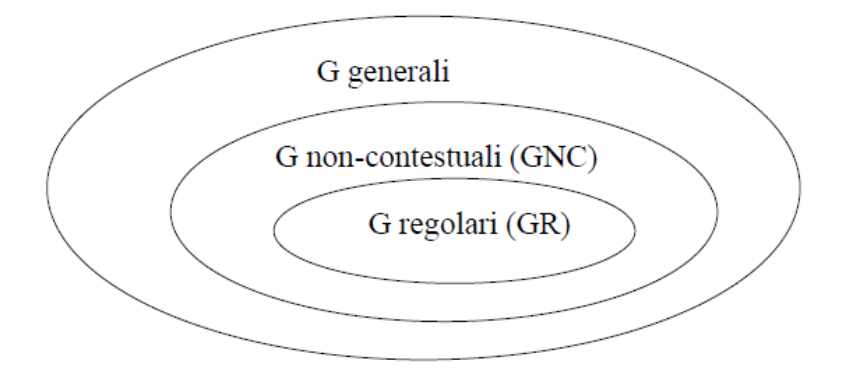
Le grammatiche sono modelli generativi di linguaggi, possiamo associare ciascuna grammatica al rispettivo automa riconoscitore del linguaggio generato:

• Tipo 0 $\to$ nessuna limitazione $\to$ MT
• Tipo 1 $\to$ limitazione cardinalità $\to$ MT
• Tipo 2 $\to$ context free $\to$ AP ND!
• Tipo 3 $\to$ grammatiche regolari $\to$ FSA

Una roba utile negli esercizi è proprio ricordarsi di queste relazioni per generare i linguaggi. Infatti il tipico esercizio ‘trova la grammatica a potenza minima per generare questo linguaggio’ può essere affrontato come ‘che tipo di automa è in grado di riconoscere questo linguaggio? A questo tipo di automa che grammatica corrisponde?‘.

Possiamo emulare una MT con una grammatica. Come? Ogni mossa è una derivazione, la derivazione ”finale” verrà effettuata solo se la MT riconosce la stringa. Utilizzeremo la ‘losanga’ $\diamond$ per separare la stringa input con quella output: input $\diamond$ output

Non è obbligatorio che la regola di derivazione $A\to B$ sia applicata a tutte le ‘A’ contemporaneamente. Si può applicare la regola $A\to B$ a tutte le ‘A’, ma si può anche non farlo. L’idea delle grammatiche è che sono un formalismo non-deterministico: tutte le possibili combinazioni di produzioni vengono provate, se si arriva ad una stringa formata da soli caratteri terminali, allora quella stringa viene detta generata dalla grammatica. 

Palindromi

E’ possibile dimostrare che se un linguaggio è palindromo, allora esiste una grammatica che lo genera.