07.Computabilità

Computabilità

Enumerazione di Gödel per MT

$f_y$ vuol dire funzione calcolabile y-esima, cioè la funzione calcolata dalla y-esima MT secondo l’enumerazione di Gödel.

Cosa significa essere computabile/calcolabile

Una funzione $f$ è calcolabile/computabile se e solo se esiste una MT che la calcola. Nel momento in cui ti chiedi se una funzione $f$ sia calcolabile o meno non sai ancora se esiste o meno la $MT$ relativa ad $f$. Ci sono funzioni per cui NON esiste una $MT$ corrispondente. Se esiste, vuol dire che, per qualsiasi input $x$, l’output della $MT$ è esattamente $f(x)$. Questo NON implica la totalità, perché le funzioni di cui studiamo la calcolabilità non sono necessariamente totali.

Esempio funzione computabile ma non totale: $g(x,y)=\{\begin{array}{l}1f_y(x)\ne \perp \\ \perp f_y(x)=\perp \end{array}$ Molti problemi, pur matematicamente ben definiti non possono essere risolti mediante procedimenti algoritmici, cioè non sono computabili (vedi l’Halting Problem). Per trovare una soluzione occorrerà caso per caso fare ricorso ad altre tecniche, tipicamente umane, senza per altro nessuna garanzia di poterla trovare.

Funzione caratteristica

$c_s(x)$ è la funzione caratteristica di un insieme. Restituisce 1 se l’elemento x appartiene all’insieme, restituisce 0 altrimenti.

Ricorsività degli insiemi:

• Ricorsivo (decidibile) se e solo se $c_s(x)$ è computabile, cioè può essere verificata da una macchina di Turing in un periodo di tempo finito.
• Ricorsivamente Enumerabile (semidecidibile) se e solo se $c_s(x)$ è computabile quando vale 1. Quando la $c_s(x)$ è 0, cioè l’elemento non appartiene all’insieme, non è necessario che la procedura si interrompa; può andare in loop per alcuni casi “non appartiene”.

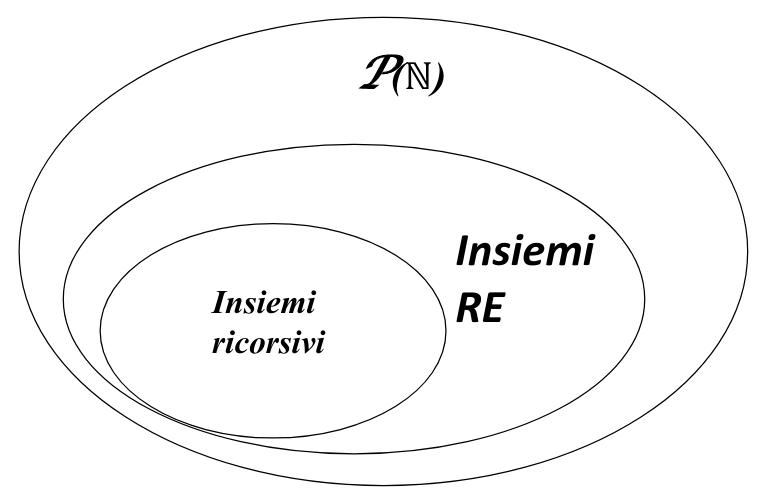
Piccolo recap: Se insieme è finito $\to$ ricorsivo. Se un insieme è ricorsivo $\to$ $c_s(x)$ computabile e totale. Se un algoritmo termina sempre $\to$ decidibile. Se un algoritmo termina sempre quando la risposta è SI, ma non necessariamente quando la risposta è NO $\to$ semidecidibile.

Halting Problem

Nessuna MT può calcolare la funzione totale seguente: $g(x,y)=\{\begin{array}{l}1f_y(x)\ne \perp \\ 0f_y(x)=\perp \end{array}$

Nessuna MT può decidere a priori se una MT (leggasi programma) si fermerà (non entrerà “in loop”) per un dato valore di ingresso. Dimostrazione: Supponiamo che g sia computabile. Allora la funzione h definita come:

$h(x)=\{\begin{array}{l}1f_x(x)=0\\ \perp otherwise\end{array}$

è anch’essa computabile. Allora esiste $x$ $\in$ N t.c. $f_x=h$. Ma allora se calcoliamo $h(x)$ abbiamo due casi: $h(x)=f_x(x)=1$, ma allora $f_x(x)=0$, che porta a $f_x(x)=\perp$ che è assurdo $h(x)=f_x(x)=\perp$, ma allora $f_x(x)=1$, che porta a $f_x(x)\ne \perp$ che è ancora assurdo Quindi h non può essere computabile e di conseguenza non può essere computabile nemmeno f.

bool halting(int i){
	if(halting(42)) while(1);
	else return true;
}

Problemi indecidibili:

No sense in putting any effort to solve an undecidable problem.

• stabilire se MT riconosce $L_1$ (indecidibile per Rice)
• Problema totalità funzione
• Problema di determinare se una generica funzione computabile è definita per almeno un valore del suo dominio. La proprietà che si vuole decidere è sicuramente posseduta da alcune funzioni calcolabili definite sull’insieme delle funzioni ma non da tutte. In base al teorema di Rice allora non è possibile stabilire se un generico algoritmo (comunque codificato) calcoli una funzione dotata della proprietà suddetta.
• Problema di determinare se una funzione ha un minimo globale
• Problema correttezza di un programma
• Problema equivalenza di due programmi
• Problema di decidere se il linguaggio accettato da una generica MT (e quindi grammatice non ristrette) è vuoto o no. Il problema non è decidibile, lo si può mostrate per riduzione dal problema della terminazione del calcolo.
• Sapere se due programmi computano la stessa funzione sapendo che terminano per ogni input (non decidibile perchè non sai se il dominio di partenza è finito)
• Un problema è irrisolvibile quando bisogna prendere in considerazione infiniti casi possibili (una funzione costante è sempre decidibile).
• Determinare se l’intersezione dei linguaggi generati da due grammatiche è vuoto
• Determinare, data una grammatica $G$ ed un insieme di grammatiche $\Gamma$ se $G\in \gamma$
• Determinare data una grammatica $G$ ed un insieme di linguaggi $\mathbb{L}$ se $L(G)\in \mathbb{L}$
• l’Alacre Castoro : determinare la MT in un insieme di MT con lo stesso numero di stati che effettua il maggior numero di passi di computazioni, alla fine terminando.
• Verificare se una MT accetta una stringa vuota
• Condizione necessaria finché $P$ sia indecidibile è che esso sia formalizzabile come il problema del calcolo di una funzione $f_P$ il cui dominio sia infinito. Non sufficiente!: ad esempio la funzione $f(x)=x+2$ definta sui numeri naturali ha dominio infinito ma è ovviamente calcolabile.

Problemi decidibili:

• domande con risposta chiusa si/no che non dipende da alcun input (RISPOSTA CHIUSA)
• Problema di stabilire se il linguaggio accettato da un FSA(e quindi grammatica regolare) è vuoto o no, usando il Pumping Lemma. Questo è equivalente di verificare la ‘emptyness di un linguaggio regolare’.
• equivalenza tra automi a stati finiti (e quindi grammatiche regolari)
• equivalenza di due polinomi
• Sapere se due programmi computano la stessa funzione sapendo che terminano per ogni input e che il dominio di input è finito.
• funzione costante
• Il problema di verificare se una formula di FOL è soddisfacibile è un problema sicuramente decidibile anche se la formula è aperta. Inoltre, se fattibile, si può provare a vedere se esiste un assegnamento per cui è vera e quindi la si può rendere effettivamente decisa.
• Ogni grammatica genera un linguaggio ricorsivamente enumerabile: questo è ovvio se si prende in considerazione la MT che da quella grammatica genera stringhe del linguaggio. La funzione che è calcolata dalla MT ha come immagine l’insieme di tutte le stringhe del linguaggio, quindi per definizione è ricorsivamente enumerabile.
• Una formula logica chiusa (formula in cui o non compaiono variabili o tutte le variabili presenti sono vincolate a un quantificatore) è sempre o vera o falsa, quindi decidibile, anche se non è detto che si sappia il suo valore di verità.
• Una funzione definita su un dominio finito è sempre calcolabile e decidibile essendo descrivibile mediante una tabella finita. Esiste ovviamente sempre una Macchina di Turing che “calcola” una tabella finita di valori.

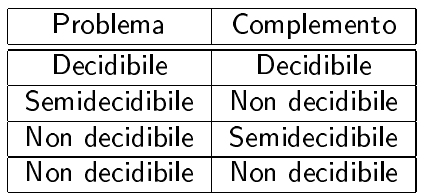
Problemi semidecidibili:

• Sapere se due programmi che terminano per ogni input computano funzioni differenti
• Sapere se due funzioni definite sullo stesso dominio sono differenti

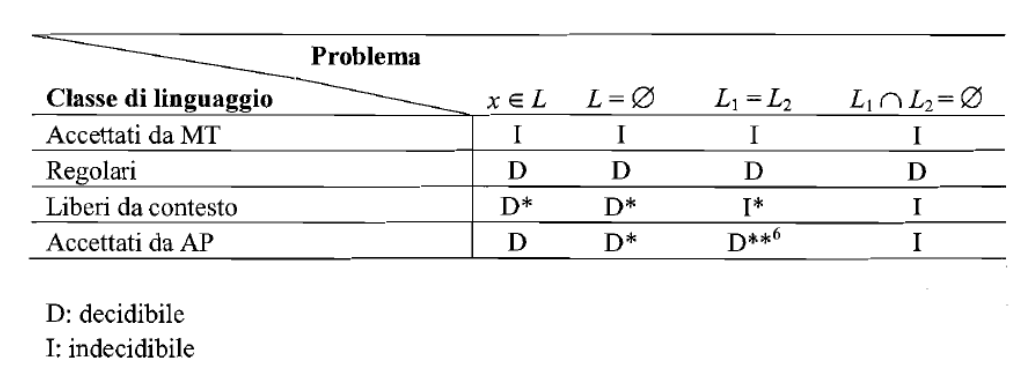
Metodi per determinare decidibilitá

Teorema di Rice

Sia $\mathbb{F}$ un insieme di funzioni computabili. Per ogni funzione di $\mathbb{F}$ possiamo trovare una MT. L’insieme $\mathbb{S}$ di tutti e soli indici delle MT che calcolano le funzioni di $\mathbb{F}$ è:

• decidibile se solo se $\mathbb{F}$ è banale (cioè vuoto o totale).
• indecidibile altrimenti.

Spiegato a mo’ di spaghettata: dire se un certo insieme di funzioni condividono o meno una stessa proprietà è indecidibile, tranne nei casi in cui tale insieme è banale.

Conseguenza peso del Teorema di Rice:

• Non possiamo stabilire l’equivalenza di due programmi.

NB: Tutte le proprietà che riguardano una caratteristica strutturale (numero di stati, sullo spazio occupato, sul numero di righe di codice) e non comportamentale di una MT, NON sono proprietà della funzione calcolata dalla MT e quindi non si può usare Rice.

Riduzione

**come ricordarsi come funziona la Riduzione di A $\to$ B

int problemA(){
	//operations
	problemB();
	//operations
}

Dati A e B. Riduco A in B e dico che:

• se B non è decidibile, allora neanche A lo è
• se A è decidibile, anche B è decidibile Cioé:
• Conosco un problema indecidibile che è un caso particolare del mio problema: il mio problema è indecidibile
• Conosco un problema decidibile di cui il mio problema è un caso particolare: il mio problema è decidibile

Diagonalizzazione

Si basa sulla diagonalizzazione di Cantor. Tosta.