prof: Barenghi Alessandro
Dynamic Programming
Generalizzazione di divide et impera. In generale quando dei sottoproblemi di un problema sono ‘uguali’ alla soluzione del problema . Ci sono problemi in cui tali sottoproblemi non ‘si sovrappongono’ in altri casi invece si, e qui entra la DP che fa uso di ‘look up’ , cioè si salva le informazioni già calcolate.
Algoritmi Greedy
Sono algoritmi che analizzano ottimi locali.
Complessità computazionale
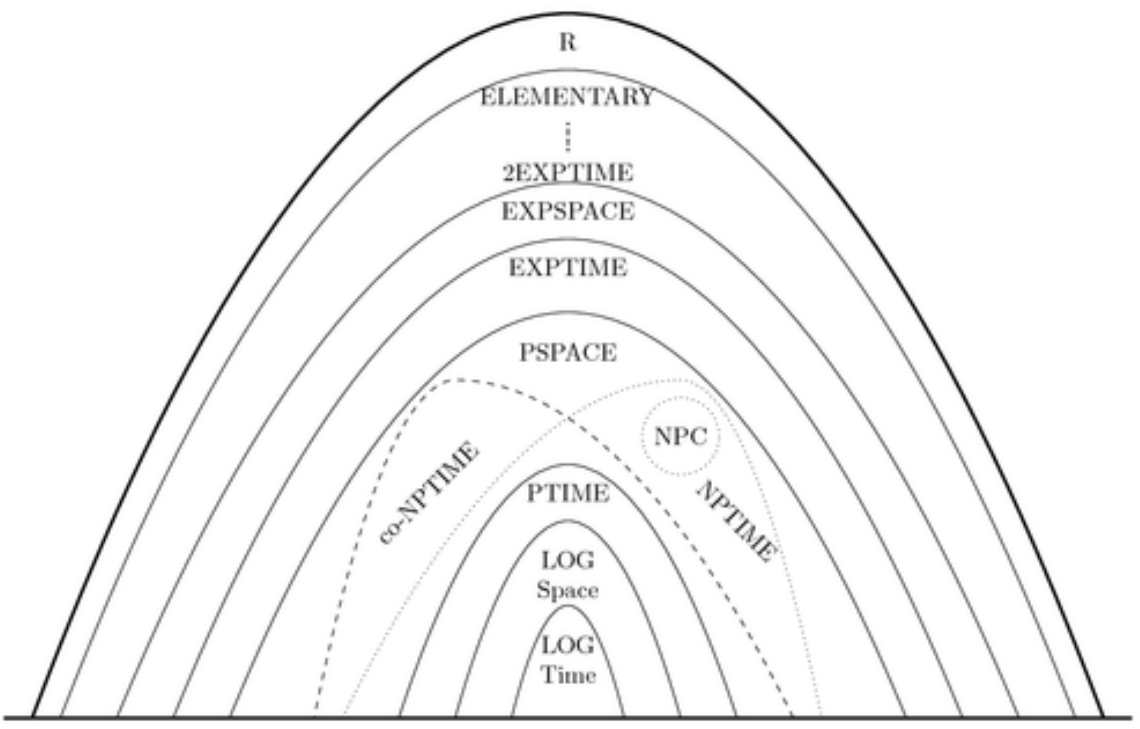
Posso classificare i problemi in base alla loro complessità?
- : insieme di tutti i problemi per cui esiste un algoritmo in
- come ma solo per MT non deterministiche.
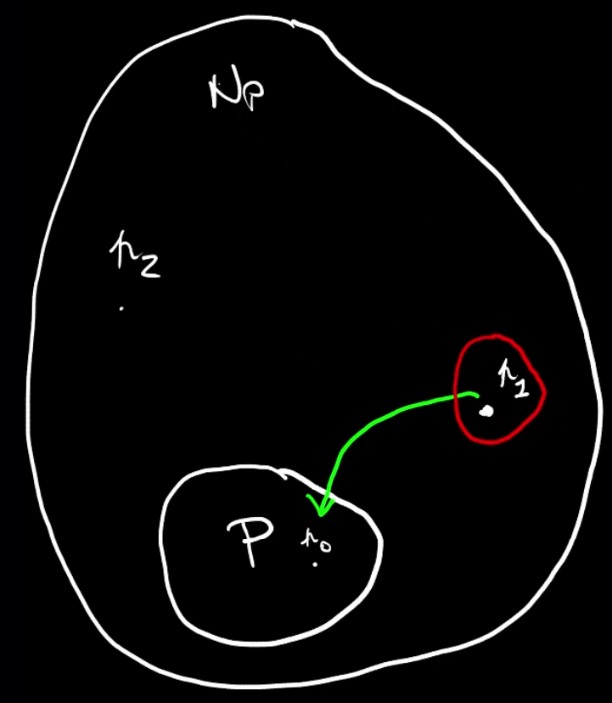
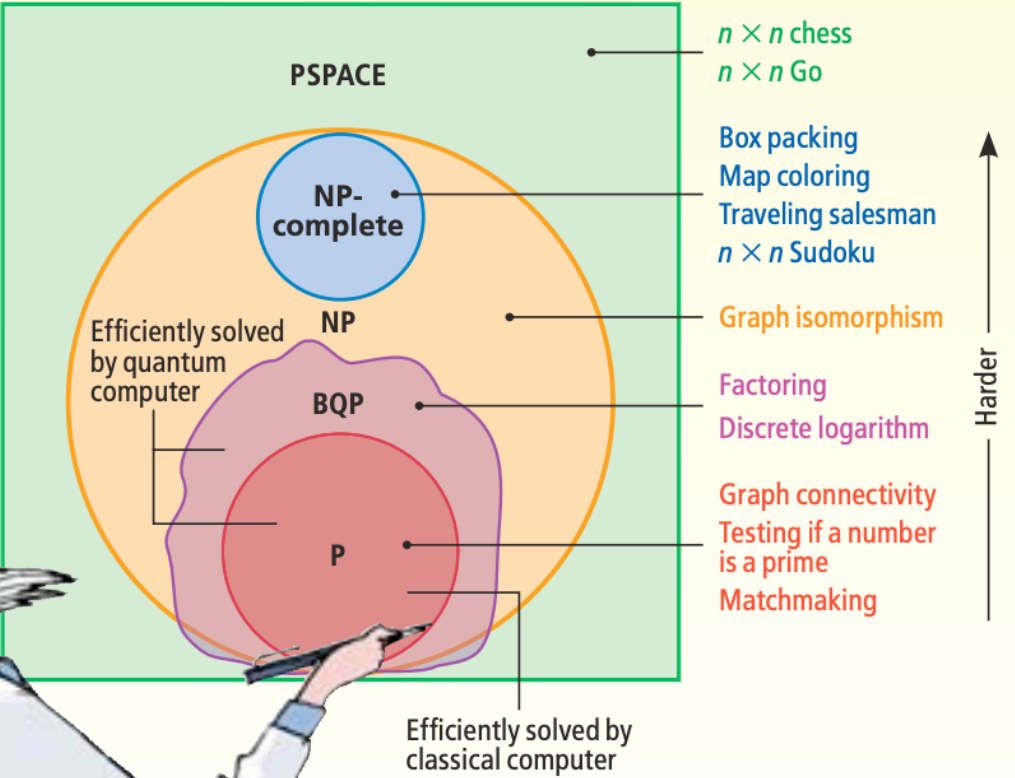
Problemi polinomiali:
Sovrainsieme dei problemi risolvibili con una MT non deterministica in maniera polinomiale.
 {width=50%}
{width=50%}
Ricordiamoci che una MT ND fa tutto quello che fa una MT D .. letteralmente è come se provasse tante MT D in parallelo raggiungendo la soluzione. Il fatto è che noi per certi problemi non riusciamo a risolverli con una MT D e basta.
Esiste un algoritmo che risolve i problemi di NP in P? cioè .. P=NP?
-
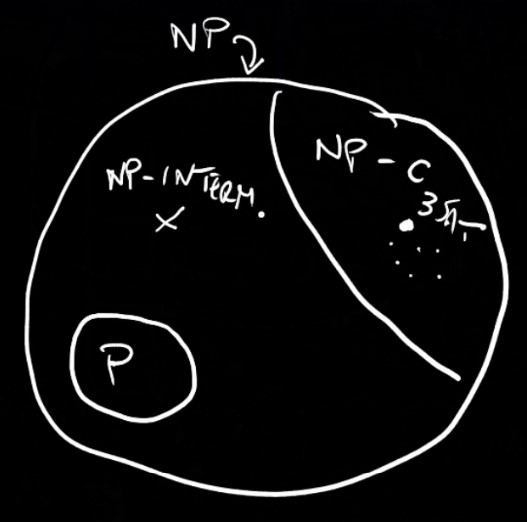
Riduzione di Turing: riduco prob. A in B, significa che A può essere risolto sapendo risolvere B. Cioè effettivamente è come se risolvessi la funzione A() con dentro la funzione B().
-
Riduzione di Cook: riduzione di Turing ma chiamo B in A un numero polinomiale di volte.
Due problemi hanno stessa complessità se riduco A in B e riduco B in A.
 {width=50%}
{width=50%}
 {width=50%}
{width=50%}
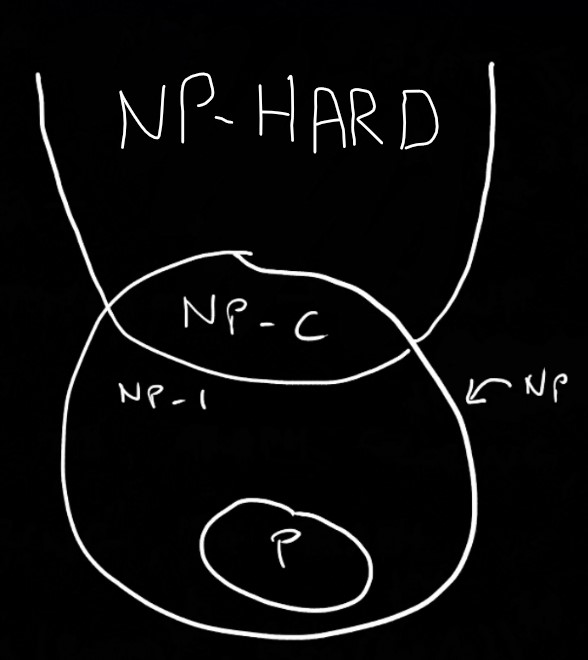
Per ora siamo abbastanza convinti che
se P fosse NP, noi potremmo dire che risolvere una formula 3-sat sarebbe difficile tanto quanto verificarne la correttezza. Che tradotto significherebbe dire che trovare una dimostrazione è tanto difficile tanto quanto dimostrarne la correttezza, concetto che va un tantino in contrasto con quello fin’ora fatto dall’umanità.
Se è vero che trovare la dimostrazione di NP=P è tanto difficile tanto quanto verificarne la correttezza perchè non ci siamo ancora riusciti?
 {width=50%}
{width=50%}
 {width=50%}
{width=50%}