01.Cinematica del punto

Cinematica del punto

Notazione con Coordinate cartesiane

$\vec{P}=x\vec{i}+y\vec{j}$ $\vec{V}=\dot{x}(t)\vec{i}+\dot{y}(t)\vec{j}$ Dove $\vec{i}$ e $\vec{j}$ sono i vettori unitari del sistema di riferimento (versori).

Notazione con Numeri Complessi

$\vec{P}=x+yi$ $\vec{V}=\dot{x}(t)+\dot{y}(t)i$ Dove $i$ è l’unità immaginaria. Di conseguenza il numero complesso può a sua volta essere scritto con la notazione polare…

Notazione Polare

$\vec{P}=P{e}^{\theta i}$ $\vec{V}=\dot{P}{e}^{\theta i}+P\dot{\theta }i{e}^{\theta i}$

Ripasso prodotto vettoriale e scalare

Prodotto vettoriale

$\vec{c}=\vec{b}\wedge \vec{a}$ Il prodotto vettoriale di due vettori è un terzo vettore con direzione ricavabile tramite la regola della mano destra e modulo $ba\sin (\alpha )$, dove $\alpha$ è l’angolo compreso tra $\vec{b}$ e $\vec{a}$ . Verrà utilizzato spesso per calcolare la velocità tangenziale di un punto che si muove lungo orbita circolare di raggio R ad esempio e con una certa velocità angolare.

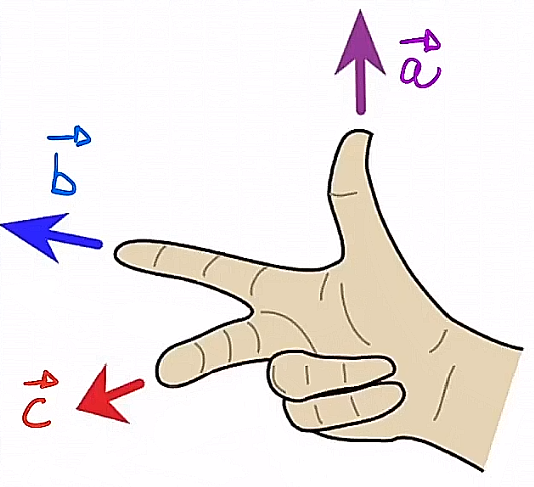
Prodotto scalare

$\vec{c}=\vec{b}\cdot \vec{a}$ Il prodotto scalare di due vettori è uno scalare uguale a $ba\cos (\alpha )$, dove $\alpha$ è l’angolo compreso tra $\vec{b}$ e $\vec{a}$ . Il prodotto scalare verrà spesso utilizzato per calcolare la potenza di coppie e forze o per calcolare la derivata dell’energia cinetica.

Ripasso regola di Kramer per sistemi

Comoda in alcuni casi per risparmiare conti.

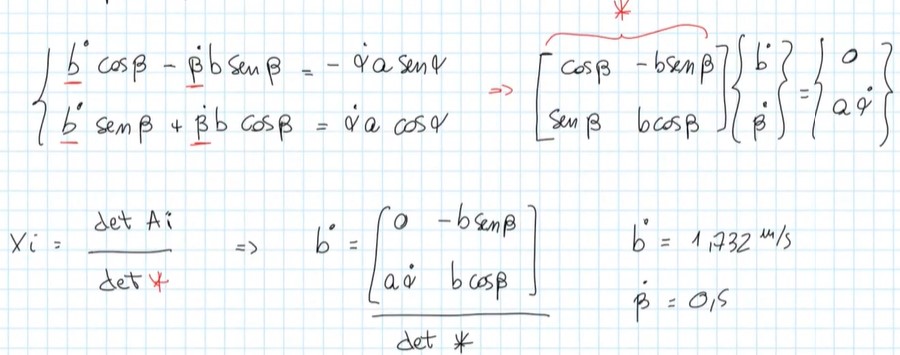
Rivals per la velocità

La velocità assoluta di un punto qualsiasi di un corpo rigido rispetto a un altro punto qualsiasi $O$ è data dalla sovrapposizione di 2 contributi:

1. contributo di traslazione di un suo punto arbitrario $O$
2. contributo di rotazione del corpo rigido attorno al punto scelto, rispetto ad un asse perpendicolare al piano del moto

$\vec{x}=\overrightarrow{v_o}+\vec{\omega }\wedge (X-O)$

Rivals per l’accelerazione

L’accelerazione assoluta di un punto qualsiasi di un corpo rigido rispetto ad un altro punto qualsiasi $O$ è data dalla sovrapposizione di 3 contributi:

1. contributo di traslazione o trascinamento di un suo punto arbitrario $O$
2. accelerazione tangenziale
3. accelerazione centripeta $\vec{x}=\overrightarrow{a_o}+\dot{\vec{\omega }}\wedge (X-O)+\vec{\omega }\wedge [\vec{\omega }\wedge (X-O)]$

Moti relativi per le velocità

$(P-O)=(O_1-O)+(P-O_1)$

scrivendo $(P-O_1)=x_p\vec{i}+y_p\vec{j}$ posso derivare tranqui $(P-O)$ e $(O_1-O)$ ma non $(P-O_1)$ in quanto i primi 2 avranno fissi i versori $\vec{i}$ e $\vec{j}$ mentre l’ultima componente non avrà i versori fissati, ma essi potranno cambiare ‘orientamento’ (poichè la terna mobile in $O_1$ può ruotare su sè stessa). Dobbiamo calcolare per l’ultima componente la derivata di un prodotto quindi $\leftarrow$ ma questo sarà sbatti.

$\dot{x_p}\vec{i}+\dot{y_p}\vec{j}=\dot{x_{o_1}}\vec{i}+\dot{y_{o_1}}\vec{j}+\dot{x_{p_1}}\vec{i}+\dot{y_{p_1}}\vec{j}+x_{p_1}\vec{\dot{i}}+y_{p_1}\vec{\dot{j}}$

La dimostrazione consiste di vedere la terna come ‘un corpo rigido’ e utilizzare Rivals per le velocità: il tutto per calcolare le 2 derivate rispetto al tempo dei versori del sistema di riferimento mobile. Sappiamo per Rivals per le velocità che $\vec{p}=\overrightarrow{v_{o_1}}+\vec{\omega }\wedge (P-O_1)$ , quindi possiamo eguagliare le equazioni e dire che $x_{p_1}\vec{\dot{i}}+y_{p_1}\vec{\dot{j}}$ è esprimibile come $\vec{\omega }\wedge (P-O_1)$ . Quindi il contributo dato dalle componenti con $\vec{\dot{i}}$ e $\vec{\dot{j}}$ può essere espresso come un contributo di rotazione rispetto al centro della terna. Nota che $\omega =\dot{\varphi }\vec{k}$ dove $\varphi$ è l’angolo dei vettori $\vec{i}$ e $\vec{j}$ della terna centrata in $O_1$ rispetto ai vettori assoluti della terna centrata in $O$ .

Formule di Poisson

Quindi eccoci con le formule di Poisson: $\dot{\vec{i}}=\vec{\omega }\wedge \overrightarrow{i_1}$ $\dot{\vec{j}}=\vec{\omega }\wedge \overrightarrow{j_1}$

e ci consentono di calcolare le 2 derivate rispetto al tempo dei versori del sistema di riferimento mobile.

Per concludere, la derivata di: $(P-O)=(O_1-O)+(P-O_1)$ sarà:

$\overrightarrow{v_p}=\overrightarrow{v_{o_1}}+\overrightarrow{v_{p_{rel}}}+\omega \wedge (P-O_1)$ da notare che il primo e l’ultimo (il terzo) componente della equazione precedente si tratta del cosiddetto contributo di trascinamento e può essere visto come “la velocità che avrebbe il punto $p$ se fosse inchiodato con la terna mobile”.

Teorema dei moti relativi per le accelerazioni (o teo. di Coriolis)

Tenendo in considerazione che $\omega \wedge (P-O_1)$ derivando sarà $\dot{\omega }\wedge (P-O_1)+\omega \wedge \dot{(P-O_1)}$ e che $\frac{\overrightarrow{v_{p_{rel}}}}{dt}={\vec{a}}_{p_{rel}}+\vec{\omega }\wedge \overrightarrow{v_{p_{rel}}}$ otterremo: $\overrightarrow{a_p}=\overrightarrow{a_{o_1}}+\dot{\vec{\omega }}\wedge (P-O_1)+\vec{\omega }\wedge [\vec{\omega }\wedge (P-O_1)]+\overrightarrow{a_{p_{rel}}}+2(\vec{\omega }\wedge \overrightarrow{v_{p_{rel}}})$ che può essere vista come:

$\overrightarrow{a_p}={\vec{a}}_{p_{trascinamento}}+\overrightarrow{a_{p_{rel}}}+\overrightarrow{a_{p_{coriolis}}}$

cioè:

${\vec{a}}_{p_{trascinamento}}=\overrightarrow{a_{o_1}}+\dot{\vec{\omega }}\wedge (P-O_1)+\vec{\omega }\wedge [\vec{\omega }\wedge (P-O_1)]$ dove si può evidenziare la componente di traslazione, la componente di accelerazione tangenziale e la componente di accelerazione normale $\vec{\omega }\wedge [\vec{\omega }\wedge (P-O_1)]$ .

Evidenziamo inoltre la componente di accelerazione di Coriolis $2(\vec{\omega }\wedge \overrightarrow{v_{p_{rel}}})$ la quale si annulla per $\vec{\omega }=0$ e ${\vec{v}}_{rel}=0$ o nel caso in cui $\vec{\omega }$ e ${\vec{v}}_{rel}$ sono paralleli tra loro, situazione possibile solo nello spazio 3D e non nel piano.