01.Sintesi reti combinatorie

Sintesi reti combinatorie

Obiettivo? Ridurre complessitá di reti combinatorie. Metodologie di sintesi:

• Karnaugh
• Quine-Mc Cluskey

Karnaugh

Basically formula di riduzione $az+a^{\prime }z=z$ applicato in maniera grafica.

Distanza di Hamming

“The purpose of computation is insight, not numbers”

• Richard Hamming

La distanza di Hamming è il numero di bit che cambiano tra due numeri espressi in binario. La regola di riduzione consiste nel identificare i termini che hanno distanza di Hamming unitaria.

Karnaugh segue un procedimento grafico, basato su una tabella. La tabella é come se fosse infinita, cioé la prima riga in alto segue l’ultima riga in basso, la prima colonna a sinistra segue l’ultima colonna destra. Le colonne differiranno per una unitá sulla distanza di Hamming, esempio a due dimensioni: 00, 01, 11, 10 ; Due tipi di implicanti:

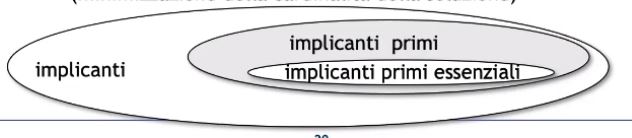
• Implicante primo = raggruppamento massimo di uni.
• Implicante primo essenziale = implicante primo unico (tra tutti gli implicanti primi) a coprire uno specifico uno.

Divido l’algoritmo in 2 fasi principali:

• l’espansione in cui identifico gli implicanti e gli implicanti essenziali.
• la copertura, cioé scelta del minor numero di implicanti primi. Chiaramenti dovró per forza prendere quelle essenziali, in quanto al termine di questa fase non ci dovranno essere 1 scoperti.

Potremmo utilizzare i simboli di don’t care ”-” per indicare bit che non ci interessano. Come trattiamo i DC? all’inizio come se fossero 1 (espansione), poi dopo (copertura) come se fossero 0. Quando utilizziamo i DC? ad esempio quando in una rete combionatoria non é osservabile sotto certe configurazioni o non é necessario calcolarne la funzione. Karnugh viene utilizzato con poche variabili, di piú dovremmo ricorrere a piú dimensioni .. cioé piú tabelle.

Metodo di Quine McCluskey

In sostanza é come Karnaugh ma utilizzando solo tabelle e ‘skippando’ l’uso di un metodo grafico, concentrandosi su un metodo tabulare. Passaggi risolutivi sono:

1. Riordino dei mintermini.
2. Si notano i mintermini non marcati (di conseguenza non sono implicanti primi).
3. Successivamente si possono trovare le configurazioni non marcate; questi costituiscono degli implicanti primi.
4. Si passa alla tabella di copertura.
5. Si cerca di ridurre la tabella di copertura, notando che alcune colonne hanno una sola marca: sono gli implicanti essenziali. Di conseguenza applico tutte le regole di dominanza*.
6. La tabella di copertura ridotta e’ vuota, è una copertura minima e (magari) unica.

Dominanza

La ‘dominanza’ esiste di due tipi:

• Dominanza di riga: $P_i$ domina $P_j$ sse copre almeno i termini di $P_j$ e il costo di $P_j$ é maggiore o uguale a quello di $P_i$. Rimuovo quindi tutta la riga dominata mantenendo la dominante.
• Dominanza di colonna: quando la copertura di un mintermine induce la copertura di un altro mintermine. Quella piú scomoda da imparare. Rimuovo quindi la copertura del mintermine dominato. Il senso è ‘mantengo solo la colonna del mintermine il quale sono sicuro, coprendolo, implica anche la copertura del mintermine corrispondente alla colonna eliminata’.

McCluskey con funzioni non completamente specificate

Fai come al solito e arrivato alla tabella di copertura non consideri affatto il mintermine del $D{C}_{set}$ (Don’t Care Set).