04.Aritmetica

Aritmetica

Standard ieee 754

Standard per scrivere numeri con la virgola mobile in binario. Nel caso di singola precisione: $(-1{)}^{S}1,mantissa{2}^{E+127}$

E poi $S$ $E$ $M$ : con $S$ é logicamente a 1 bit, $E$ a 8 bit e $M$ a 23 bit. Nel caso a doppia precisione $S$ é 1 bit, $E$ 11 bit e $M$ 52 bit.

Somma tra numeri binari a virgola mobile

Per sommare due numeri in virgola mobile con diverso esponente bisogna considerare la mantissa del numero con più piccolo esponente e farla scorrere a destra (sommando un 1 ad ogni passo all’esponente) fino a quando i due esponenti non si equivalgono. Si esegue l’operazione di somma (algebrica) tra le mantisse per determinare il valore ed il segno del risultato e se necessario si normalizza il risultato.

Moltiplicazione di numeri binari

La fai come alle elementari ma in complemento a 2. L’unica accortezza é di ricordare che nel caso di XY ci sono 4 casi:

• X positivo, Y positivo no problem
• X é negativo, Y positivo no problem
• X positivo, Y negativo li scambi e moltiplichi uguale (oppure calcoli con i segni invertiti)
• X negativo, Y negativo, calcoli il prodotto tra i loro valori assoluti altrimenti il risultato é sbagliato.

la morale é che il moltiplicatore non deve essere negativo

Algoritmo radici positive e negative

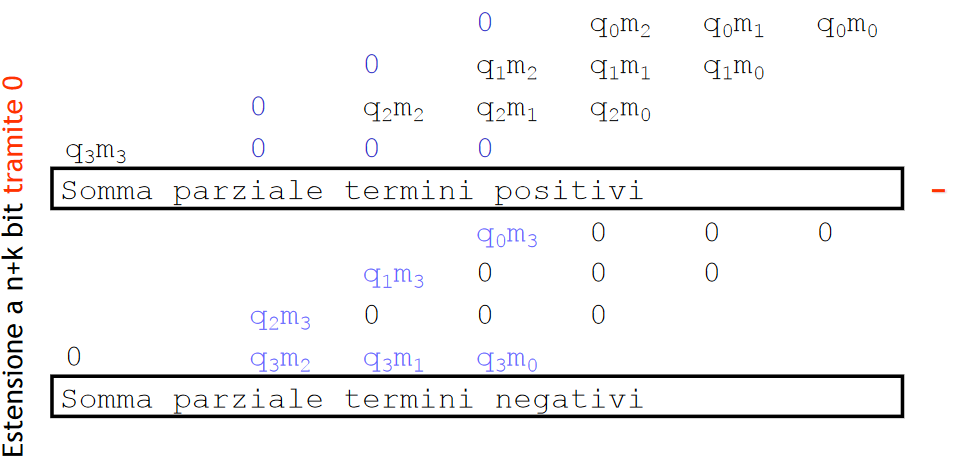
Alternativamente alla classica moltiplicazione, in caso di moltiplicatore negativo si puó usare l’algoritmo delle radici positive/negative . Si tratta di scomporre la matrice iniziale in due sottomatrici, una con i soli termini negativi, l’altra con solo quelli positivi. Il risultato è dato dalla differenza dei due risultati parziali.

Codifica di Booth per le moltiplicazioni

Il concetto base della codifica di Booth é di codificare il moltiplicatore per ridurre i prodotti parziali e semplificare quindi la rete combinatoria/conti. La bellezza della codifica di Booth é che adatto per operandi di qualsiasi segno. La codifica di Booth é disponibile in due gusti:

• Radix 2
• Radix 4

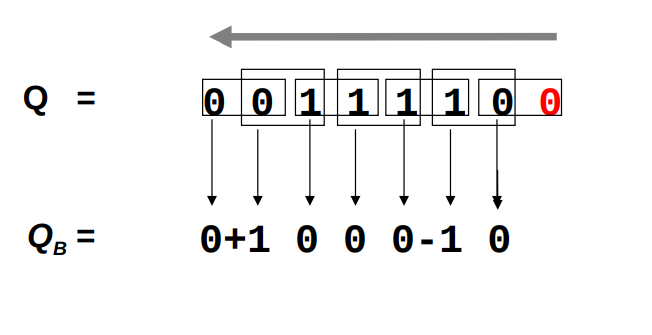
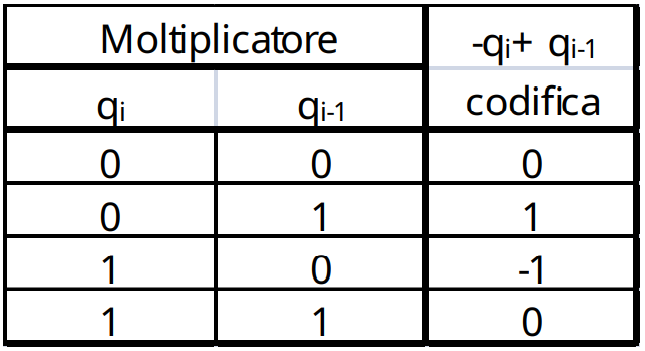
Sia per Radix 2 che Radix 4 si aggiunge uno zero a destra del numero. E poi si divide il numero in gruppetti da 2 (radix2) o 3 (radix3) e si converte in base alle seguenti tabelle ciascun gruppettino. Poi si effettua la moltiplicazione stile elementari.

Radix 2

{width=50%}

{width=50%}

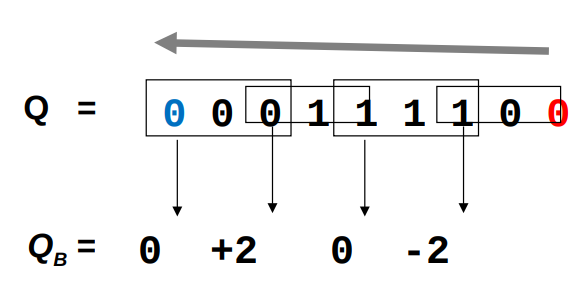
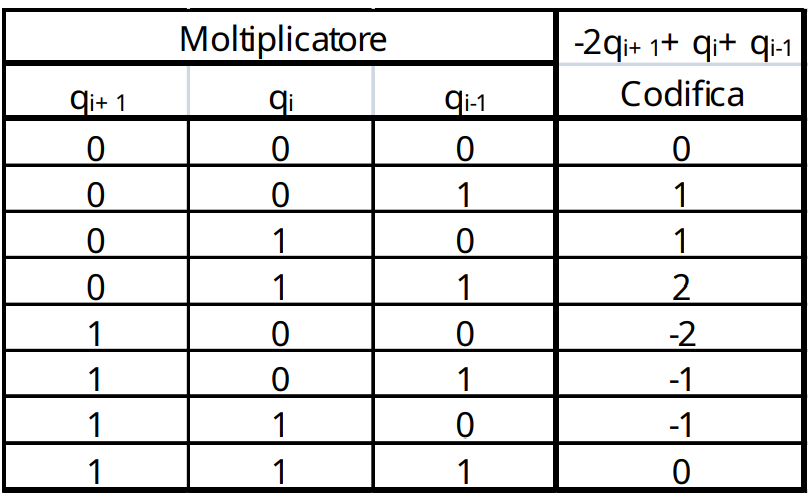
Radix 4

{width=50%}

{width=50%}

Nota come anche Radix4 alla fine risulti comodo:

• 1 si tratta di ricopiare il numero
• -1 si tratta di invertire e sommare 1 (complemento)
• -2 si tratta di shiftare verso sinistra di una posizione il numero e di calcolarne il complemento
• 0 solo zeri