08. CUDA Kernel optimizations

CUDA Kernel optimizations

To maximize compute performance in CUDA kernels there are common patterns and “rules” that we can follow.

Optimization	Strategy	Benefit to Compute Cores	Benefit to Memory
Maximizing occupancy	Tune usage of SM resources (threads per block, shared memory per block, registers per thread)	More work to hide pipeline latency	More parallel memory accesses to hide DRAM latency
Enabling coalesced global memory accesses	Transfer between global and shared memory in a coalesced manner; Rearrange thread-to-data mapping and data layout	Fewer pipeline stalls waiting for global memory accesses	Less global memory traffic and better utilization of bursts/cache lines
Minimizing control divergence	Rearrange thread-to-work/data mapping and data layout	High SIMD efficiency (fewer idle cores during SIMD execution)	-
Tiling of reused data	Place reused data within a block in shared memory or registers	Fewer pipeline stalls waiting for global memory accesses	Less global memory traffic
Privatization	Apply partial updates to private data copies before updating the universal copy	Fewer pipeline stalls waiting for atomic updates	Less contention and serialization of atomic updates
Thread coarsening	Assign multiple units of parallelism to each thread	Less redundant work, divergence, or synchronization	Less redundant global memory traffic

Maximizing Occupancy

The goal is to hide memory latencies by fully utilizing all available resources (threads and resources). This allows the GPU scheduler to continue executing work, effectively hiding the latency of memory operations from both compute and memory perspectives. A starting point to minimize kernel execution time is to maximize SM occupancy. When manually tuning the block thread size, consider the following guidelines:

• Ensure the block size is a multiple of the warp size.
• Avoid using small block sizes.
• Adjust the block size according to the kernel’s resource requirements.
• The total number of blocks should significantly exceed the number of SMs.
• Engage in systematic experiments to find the best configuration.

Memory Access

Efficient memory access patterns are crucial for performance.

Coalesced memory access refers to the pattern of global memory access where threads in a warp access contiguous memory addresses.

• Applies to global memory access
• Aims to minimize the number of memory transactions
• Improves global memory bandwidth utilization

Shared memory can be used to avoid un-coalesced memory accesses by loading and storing data in a coalesced pattern from global memory and then reordering it in shared memory.

Shared memory can only be loaded by memory operations performed by threads in CUDA kernels. There are no API functions to load shared memory.

If you have an array that is larger than the number of threads in a threadblock, you can use a looping approach like this:

#define SSIZE 2592
 
__shared__ float TMshared[SSIZE]; 
 
  int lidx = threadIdx.x;
  while (lidx < SSIZE){
    TMShared[lidx] = TM[lidx];
    lidx += blockDim.x;}
 
__syncthreads();

In a naive SGEMM (simple general matrix multiply) kernel, memory access patterns can lead to non-coalesced access:

// non-coalesced memory access
__global__ void sgemm_naive(int M, int N, const float *A, const float *B, float beta, float *C) {
   const uint x = blockIdx.x * blockDim.x + threadIdx.x;
   const uint y = blockIdx.y * blockDim.y + threadIdx.y;
   // ... rest of the kernel ...
}

To ensure consecutive threads access consecutive memory locations:

// Example of a coalesced memory access pattern
__global__ void sgemm_coalesced(int M, int N, const float *A, const float *B, float *C) {
 int Row = blockIdx.y * blockDim.y + threadIdx.y;
 int Col = blockIdx.x * blockDim.x + threadIdx.x;
 if (Row < M && Col < N) {
     float Cvalue = 0.0;
     for (int k = 0; k < K; ++k) {
         Cvalue += A[Row * K + k] * B[k * N + Col];
     }
     C[Row * N + Col] = Cvalue;
 }
}

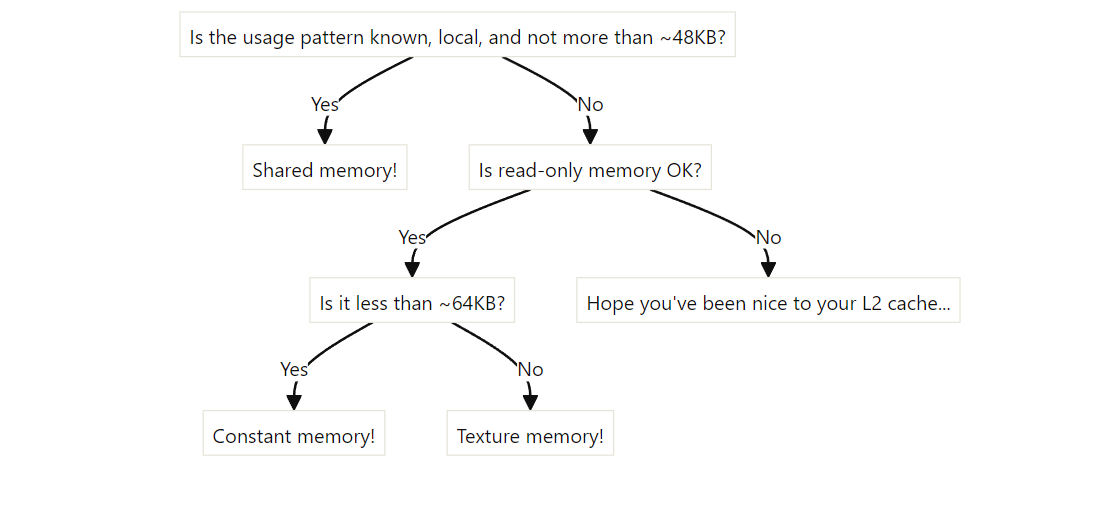
Bank Conflicts `

As said before, shared memory is useful to increase the kernel performance, but memory bank conflicts can happen if not correctly managed. Bank conflicts occur when multiple threads in a warp access different words in the same memory bank of shared memory.

• Primarily a concern for shared memory access
• Aims to prevent serialization of memory accesses within a warp
• Improves shared memory access efficiency

A basic matrix transpose without using shared memory:

__global__ void transposeNaive(float * __restrict__ odata, const float * __restrict__ idata) {
  const int x = blockIdx.x * TILE_DIM + threadIdx.x;
  const int y = blockIdx.y * TILE_DIM + threadIdx.y;
  const int width = gridDim.x * TILE_DIM;
 
  for (int j = 0; j < TILE_DIM; j+= BLOCK_ROWS)
    odata[x*width + (y+j)] = idata[(y+j)*width + x];
}

A naive solution using shared memory which gives bank collisions :

__global__ void transposeCoalesced(float *odata, const float *idata) {
  __shared__ float tile[TILE_DIM][TILE_DIM];
    
  int x = blockIdx.x * TILE_DIM + threadIdx.x;
  int y = blockIdx.y * TILE_DIM + threadIdx.y;
  int width = gridDim.x * TILE_DIM;
 
  for (int j = 0; j < TILE_DIM; j += BLOCK_ROWS)
    tile[threadIdx.y+j][threadIdx.x] = idata[(y+j)*width + x];
 
  __syncthreads();
 
  x = blockIdx.y * TILE_DIM + threadIdx.x;  // transpose block offset
  y = blockIdx.x * TILE_DIM + threadIdx.y;
 
  for (int j = 0; j < TILE_DIM; j += BLOCK_ROWS)
    odata[(y+j)*width + x] = tile[threadIdx.x][threadIdx.y + j];
}

During tile[threadIdx.y+j][threadIdx.x] something like this can happen:

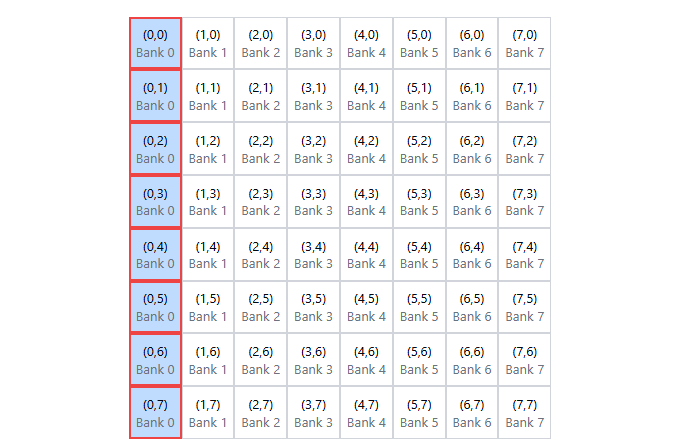
To eliminate shared memory bank conflicts __shared__ float tile[TILE_DIM][TILE_DIM+1] add padding is enough:

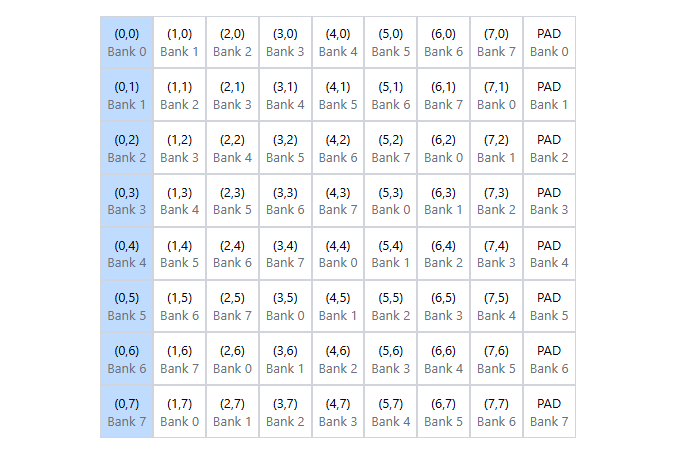
// Avoiding bank conflicts in shared memory
__shared__ float shared_data[32][33];  // Padding to avoid conflicts
int tid = threadIdx.x;
shared_data[tid][threadIdx.y] = some_value;

__global__ void transposeNoBankConflicts(float *odata, const float *idata) {
  __shared__ float tile[TILE_DIM][TILE_DIM+1]; //this +1 changed
    
  int x = blockIdx.x * TILE_DIM + threadIdx.x;
  int y = blockIdx.y * TILE_DIM + threadIdx.y;
  int width = gridDim.x * TILE_DIM;
 
  for (int j = 0; j < TILE_DIM; j += BLOCK_ROWS)
    tile[threadIdx.y+j][threadIdx.x] = idata[(y+j)*width + x];
 
  __syncthreads();
 
  x = blockIdx.y * TILE_DIM + threadIdx.x;  // transpose block offset
  y = blockIdx.x * TILE_DIM + threadIdx.y;
 
  for (int j = 0; j < TILE_DIM; j += BLOCK_ROWS)
    odata[(y+j)*width + x] = tile[threadIdx.x][threadIdx.y + j];
}

Privatization

Privatization consists in doing partial updates to private data copies before updating the universal copy.
This reduces the need for resources:

• minimizes contention and serialization of atomic operations.
• Which means less pipeline stalls

Minimizing control divergence

This strategy involves rearranging thread-to-work/data mapping and data layout to minimize situations where threads in the same warp take different execution paths.

In general we want to minimize divergent branching within a warp to avoid serialization

Now, let’s say that we have 4 threads in a warp (in reality, it’s 32, but 4 is easier to visualize) and a 1D array of data, and we want to compute a histogram. We’ll represent it like this:

[A][B][C][D][E][F][G][H][I][J][K][L][M][N][O][P]  
0  1  2  3  4  5  6  7  8  9  10 11 12 13 14 15 

Without a stride-based approach, the threads might work like this:

Thread 0: [A][B][C][D]
Thread 1: [E][F][G][H]
Thread 2: [I][J][K][L] 
Thread 3: [M][N][O][P]

This is a mis-aligned memory access but it has also consequences on control divergence. With a stride-based approach:

1. All threads are processing elements at the same stride (distance) from each other.
2. In each iteration, threads are more likely to be processing similar types of data (e.g., all at the beginning, all in the middle, etc.).
3. If there’s any pattern in the data, all threads will encounter this pattern together.
4. Even if divergence occurs, it’s more likely to affect all threads similarly, rather than causing some threads to do much more work than others.

Iteration 1:
	Thread 0: [A][ ][ ][ ] 
	Thread 1: [B][ ][ ][ ]
	Thread 2: [C][ ][ ][ ]
	Thread 3: [D][ ][ ][ ]
 
Iteration 2: 
	Thread 0: [A][E][ ][ ]
	Thread 1: [B][F][ ][ ]
	Thread 2: [C][G][ ][ ]
	Thread 3: [D][H][ ][ ]
 
Iteration 3: 
	Thread 0: [A][E][I][ ]
	Thread 1: [B][F][J][ ]
	Thread 2: [C][G][K][ ]
	Thread 3: [D][H][L][ ] 
 
Iteration 4: 
	Thread 0: [A][E][I][M]
	Thread 1: [B][F][J][N]
	Thread 2: [C][G][K][O]
	Thread 3: [D][H][L][P]

Tiling of reused data

Tiling involves dividing a large data set into smaller chunks, or tiles, and processing them in parallel. This strategy involves placing reused data within a block in shared memory or registers. It reduces pipeline stalls waiting for global memory accesses and decreases global memory traffic.

The general outline of tiling technique:

1. Identify a tile of global memory content that are accessed by multiple threads
2. The tile from global memory into on-chip memory
3. Have the multiple threads to access their data from the on-chip memory
4. Move on to the next tile

Thread Coarsening

Coarsening refers to increasing the amount of work done by each thread in a kernel.

“Instead of having many threads doing small amounts of work, fewer threads do more work each.”

This could seem counterintuitive, but for instance in the context of processing an image, instead of assigning one thread per pixel, thread coarsening would assign one thread to handle a block of pixels, reducing the total number of threads and potentially making better use of the GPU’s resources.

Thread Coarsening:

• reduces redundant work, divergence, or synchronization
• decreases redundant global memory traffic