Convolution

Convolution is a mathematical operation that combines two functions to produce a third function.

Apart from image processing (blurring, sharpening, embossing, edge detection), the convolution operation is the foundation of Convolutional Neural Networks.

It involves sliding a filter (or kernel) over an input, performing element-wise multiplication and summation at each position, resulting in a transformed output that emphasizes or detects specific features in the data.

If we assume that the dimension of the filter is $(2 r_{x} + 1)$ in the $x$ dimension and $(2 r_{y} + 1)$ in the $y$ dimension, the calculation of each $P$ element can be expressed as follows:

$P (i, j) = \sum_{m = - r_{y}}^{r_{y}} \sum_{n = - r_{x}}^{r_{x}} I (i + m, j + n) \cdot F (m, n)$

where:

$P (i, j)$ is the output pixel at position $(i, j)$ $I (i + m, j + n)$ is the input pixel at position $(i + m, j + n)$ $F (m, n)$ is the filter coefficient at position $(m, n)$
Here’s a basic CPU implementation of convolution:

void convolution_cpu(input_type *input, const input_type *filter, input_type *output, 
                     int width, int height, int filter_size, int filter_radius) {
    // Iterate over each output pixel
    for (int outRow = 0; outRow < height; outRow++) {
        for (int outCol = 0; outCol < width; outCol++) {
            input_type value = 0.0f;  
            
            // Apply the filter 
            for (int row = 0; row < filter_size; row++) {
                for (int col = 0; col < filter_size; col++) {
                    int inRow = outRow - filter_radius + row; 
                    int inCol = outCol - filter_radius + col;
                    
                    if (inRow >= 0 && inRow < height && inCol >= 0 && inCol < width) {
                        value += filter[row * filter_size + col] * 
                                 input[inRow * width + inCol];
                    }
                }
            }
            output[outRow * width + outCol] = value;
        }
    }
}

Constant memory

The convolution kernel benefits from using constant memory, which is optimized for situations where all threads read the same value, such as filter coefficients in convolution operations.

Constant Memory Benefits:
- A constant memory cannot be modified by threads during kernel execution
- The size of the constant memory is quite small (64KB) and efficient
- It is a read only cache
- Less complex hardware to manage it
- good performance only when each thread accesses the same data
- Serial access to the same location is fast.
- It’s initialized once and accessible across multiple kernel launches.
- Declared at the global level with __constant__.

#define FILTER_RADIUS 4
#define FILTER_SIZE   (FILTER_RADIUS * 2 + 1)
__constant__ filter_type constant_filter[FILTER_SIZE][FILTER_SIZE];
 
// Copy filter to constant memory
cudaMemcpyToSymbol(constant_filter, filter, FILTER_SIZE * FILTER_SIZE * sizeof(filter_type));

Symbolic Filter: Treating the filter as a symbol simplifies the kernel call.
Loop Unrolling: Fixed filter size allows compiler optimizations.

Here’s a GPU kernel using constant memory:

__global__ void convolution_constant_mem_kernel(const input_type *__restrict__ input, input_type *__restrict__ output, const int width, const int height) {
    
    const int outCol = blockIdx.x * blockDim.x + threadIdx.x;
    const int outRow = blockIdx.y * blockDim.y + threadIdx.y;
    input_type value{0.0f};
    
    #pragma unroll
    for (int row = 0; row < FILTER_SIZE; row++) {
        #pragma unroll
        for (int col = 0; col < FILTER_SIZE; col++) {
            const int inRow = outRow - FILTER_RADIUS + row;
            const int inCol = outCol - FILTER_RADIUS + col;
            if (inRow >= 0 && inRow < height && inCol >= 0 && inCol < width) {
                value += constant_filter[row][col] * input[inRow * width + inCol];
            }
        }
    }
    output[outRow * width + outCol] = value;
}

Coarsening

Coarsening involves each thread performing more work, which can improve performance:

Increased arithmetic intensity
Reduced launch overhead
Improved memory access patterns
Better resource utilization

In the context of convolution operations, coarsening can be applied by having each thread compute multiple output elements instead of one.

__global__ void convolution_constant_mem_coarsening_kernel(const input_type *__restrict__ input,
                                                           input_type *__restrict__ output,
                                                           const int width, const int height) {
    const int outCol = blockIdx.x * blockDim.x + threadIdx.x;
    const int outRow = blockIdx.y * blockDim.y + threadIdx.y;
    const int stride_col = gridDim.x * blockDim.x;
    const int stride_row = gridDim.y * blockDim.y;
 
    for (int c = outCol; c < width; c += stride_col) {
        for (int r = outRow; r < height; r += stride_row) {
            input_type value = 0.0f;
            #pragma unroll
            for (int row = 0; row < FILTER_SIZE; row++) {
                #pragma unroll
                for (int col = 0; col < FILTER_SIZE; col++) {
                    const int inRow = r - FILTER_RADIUS + row;
                    const int inCol = c - FILTER_RADIUS + col;
                    if (inRow >= 0 && inRow < height && inCol >= 0 && inCol < width) {
                        value += constant_filter[row][col] * input[inRow * width + inCol];
                    }
                }
            }
            output[r * width + c] = value;
        }
    }
}

Shared Memory Optimization

The Arithmetic Intensity analysis becomes more complex:

$OUT_TILE_DIM^{2} \cdot (2 \cdot FILTER_RADIUS + 1)^{2} \cdot 2$
Since floating point operations are executed, 4 bytes are considered Memory Access: $IN_TILE_DIM^{2} \cdot 4 = (OUT_TILE_DIM + 2 \cdot FILTER_RADIUS)^{2} \cdot 4$

Asymptotically, if $OUT_TILE_DIM ≫ FILTER_RADIUS$ :

$\frac{Operations}{Memory Access} = \frac{( 2 \cdot FILTER_RADIUS + 1 ) ^{2}}{2}$

Using a shared memory approach with tiling significantly alters how data is accessed and processed on a GPU, emphasizing efficiency and reduced global memory dependency. This method is particularly effective for operations like convolution where data reuse is high. The approach minimizes the latency of data access and maximizes the throughput by leveraging the fast shared memory on the GPU.

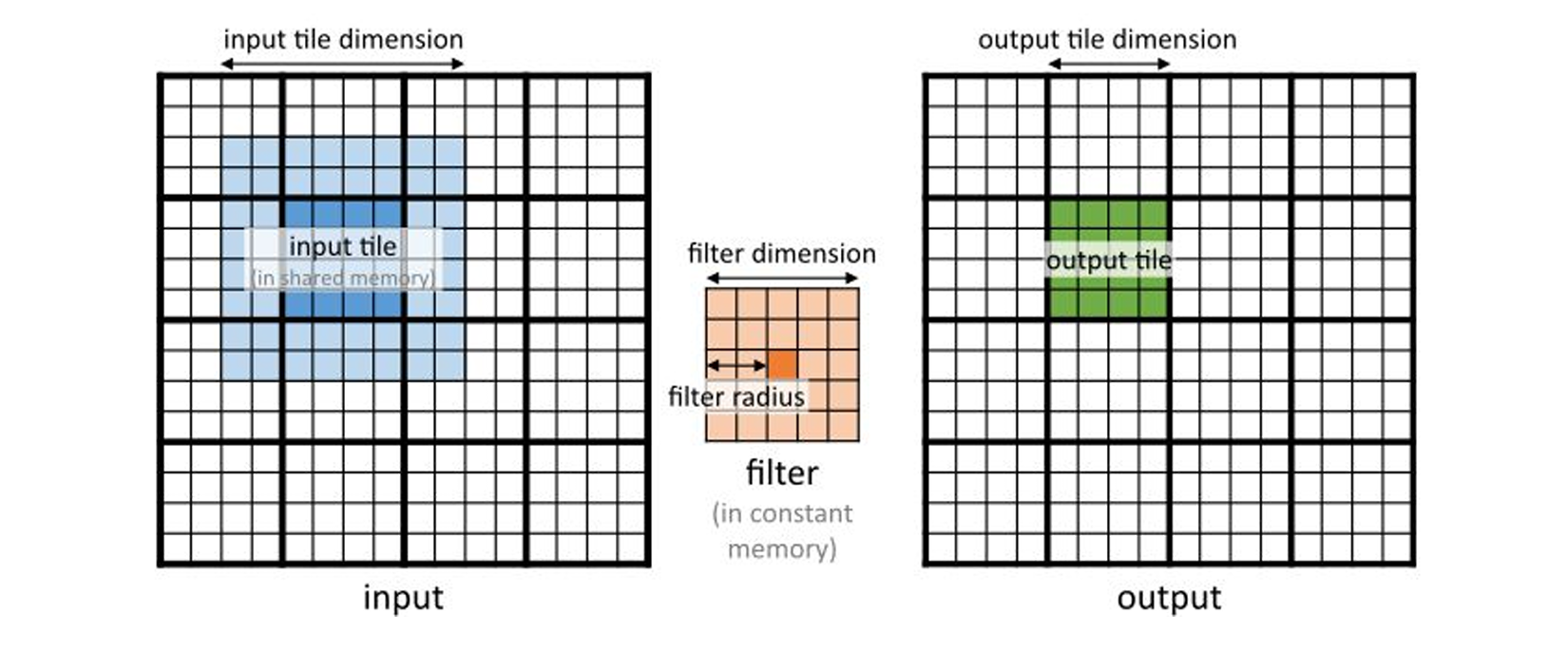
First Load the Tiles: Each thread in a block loads an element of the input image into shared memory, including necessary padding for the convolution operation. This reduces global memory accesses. After loading the data into shared memory, threads are synchronized to ensure all data is properly loaded before computation begins.

__shared__ input_type input_shared[IN_TILE_DIM][IN_TILE_DIM];
if (inRow >= 0 && inRow < height && inCol >= 0 && inCol < width) {
  input_shared[tidy][tidx] = input[inRow * width + inCol];
} else {
  input_shared[tidy][tidx] = 0.0;
}
__syncthreads();

Compute Output Elements: Each thread computes an element of the output using the data in shared memory. This computation is localized to the data loaded by the block, significantly reducing the latency associated with memory access.

const int tileCol = tidx - FILTER_RADIUS
const int tileRow = tidy - FILTER_RADIUS
 
if (tileCol >= 0 && tileCol < OUT_TILE_DIM && tileRow >= 0 && tileRow < OUT_TILE_DIM) {
  input_type output_value{0.0f};
  #pragma unroll
  for (int row = 0; row < FILTER_SIZE; row++)
  #pragma unroll
    for (int col = 0; col < FILTER_SIZE; col++)
      output_value += constant_filter[row][col] * input_shared[tileRow + row][tileCol + col];
  output[inRow * width + inCol] = output_value;
}

Using shared memory can significantly reduce global memory accesses:

__global__ void convolution_tiled_kernel(const input_type *__restrict__ input,
                                         input_type *__restrict__ output,
                                         const int width, const int height) {
    __shared__ input_type input_shared[IN_TILE_DIM][IN_TILE_DIM];
    
    // Load data into shared memory
    const int inCol = blockIdx.x * OUT_TILE_DIM + threadIdx.x - FILTER_RADIUS;
    const int inRow = blockIdx.y * OUT_TILE_DIM + threadIdx.y - FILTER_RADIUS;
    if (inRow >= 0 && inRow < height && inCol >= 0 && inCol < width) {
        input_shared[threadIdx.y][threadIdx.x] = input[inRow * width + inCol];
    } else {
        input_shared[threadIdx.y][threadIdx.x] = 0.0;
    }
    __syncthreads();
 
    // Compute output elements
    const int tileCol = threadIdx.x - FILTER_RADIUS;
    const int tileRow = threadIdx.y - FILTER_RADIUS;
    if (tileCol >= 0 && tileCol < OUT_TILE_DIM && tileRow >= 0 && tileRow < OUT_TILE_DIM) {
        input_type output_value = 0.0f;
        #pragma unroll
        for (int row = 0; row < FILTER_SIZE; row++) {
            #pragma unroll
            for (int col = 0; col < FILTER_SIZE; col++) {
                output_value += constant_filter[row][col] * 
                                input_shared[tileRow + row][tileCol + col];
            }
        }
        output[inRow * width + inCol] = output_value;
    }
}

Caching Halo Cells

Halo cells are data that come from other tiles: upon running it is very likely that these data are already available in the L2 cache.

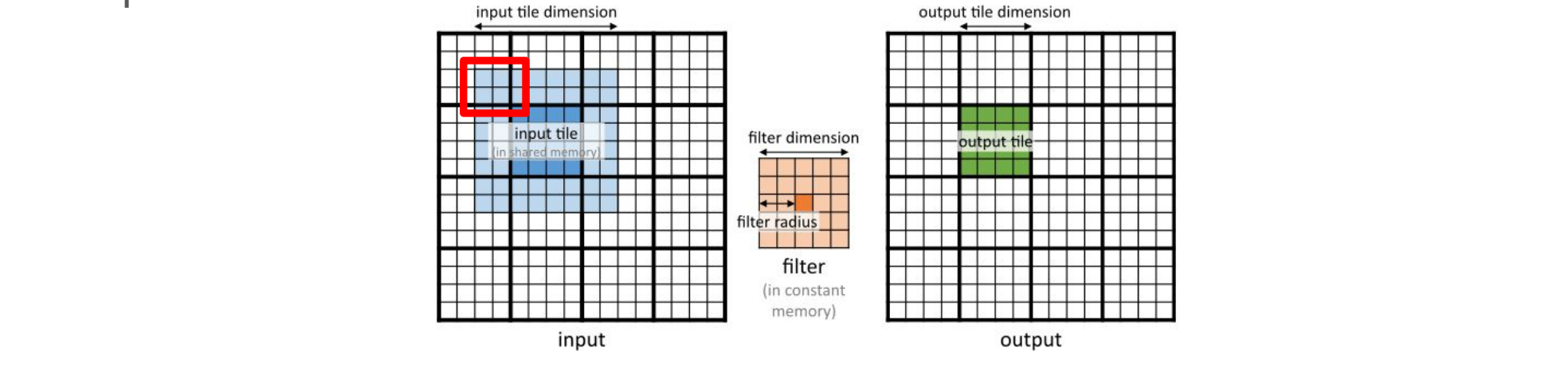
This technique loads only the internal part of the tile into shared memory, assuming halo cells are in L2 cache:

if (sharedRow >= 0 && sharedRow < TILE_DIM && sharedCol >= 0 && sharedCol < TILE_DIM) {
    // Shared memory access
    PValue += constant_filter[fRow][fCol] * input_shared[sharedRow][sharedCol];
} else {
    // Global memory access for halo cells
    int globalRow = row - FILTER_RADIUS + fRow;
    int globalCol = col - FILTER_RADIUS + fCol;
    if (globalRow >= 0 && globalRow < height && globalCol >= 0 && globalCol < width) {
        PValue += constant_filter[fRow][fCol] * input[globalRow * width + globalCol];
    }
}

Due to conditional statements handling halo and boundary conditions there is a a lot of Branch Divergence, which increase instruction count and reduce performance. Compiler’s Role: the compiler generates a substantial number of instructions to manage this complexity, which can aggravate thread divergence.

blog.martino.im

Explorer

09.Convolution

Convolution

Constant memory

Coarsening

Shared Memory Optimization

Caching Halo Cells

Graph View

Table of Contents

Backlinks