01.Introduction to MIDA1

Introduction

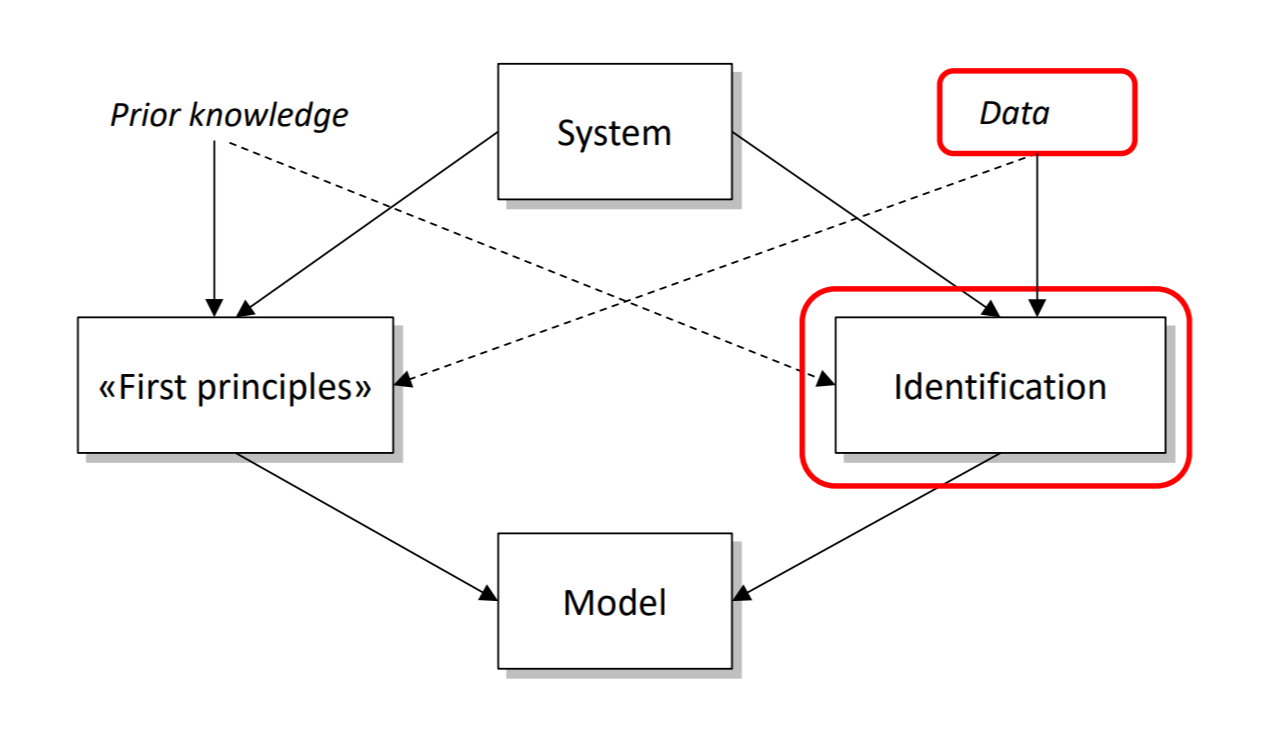
The goal of this course is to provide a framework for black-box modelling of I/O dynamical systems and time series. In engineering you usually start from principles and obtain the model. Here we use the data as a source for information to build the model

Stochastic process

The purpose of making predictions/identification on the future behavior of a signal requires taking into account the uncertainty in the model. This leads us to the need for a new concept, the stochastic process $SP$, which extends the concept of random variables to signals.

A stochastic process $SP$ is a $n$ infinite sequence of random variables that depend on the outcome of a random experiment.

In this context is important to refresh this stuff:

• Mean: $E[v]$. Key property of expected value $E[{\alpha }_1{v}_1+{\alpha }_2{v}_2]={\alpha }_{1}E[v_1]+{\alpha }_{2}E[v_2]$
• Variance: $E[(v-E[v]{)}^2]\ge 0$
• Covariance:

$\gamma (t_1,t_2)=E[(v(t_1,s)-m(t_1))(v(t_2,s)-m(t_2))]$ The covariance function is a useful statistical measure that indicates how two samples of the same stochastic process change together (“covary”). If (for example) the SP is periodic the correlation is very high. Remember also that the covariance between two functions is:

$\gamma (\tau )=E[(y_1(t)-{\mu }_1)(y_2(t+\tau )-{\mu }_2)]$ While the formula to compute the correlation function $\tilde{\gamma }(\tau )$ is:

$\tilde{\gamma }(\tau )=E[v_1(t)v_2(t-\tau )]=\gamma (\tau )+{\bar{\mu }}_1{\bar{\mu }}_2$

$\tilde{\gamma }(\tau )=E[y(t)y(t-\tau )]=\gamma (\tau )+{\bar{\mu }}^2$

We will focus on Stationary Stochastic Process ($SSP$) $y(t)$ which have the following characteristics:

• $m(t)=m\forall t$ “any realization will be a constant outcome”

• ${\gamma }_y(t_1,t_2)$ depends only on $\tau =t_2-t_1$ and can therefore be indicated with ${\gamma }_y(\tau )$. This basically means “it’s not important when you take the samples but only the absolute shift between the two”. Also (always if $y(t)$ is stationary) the covariance ${\gamma }_y$ has these proprieties:

  • $\gamma (0)=E[(v(t,s)-m{)}^2]\ge 0$ positivity
  • $|\gamma (\tau )|\le \gamma (0),\forall \tau$ not increasing
  • $\gamma (\tau )=\gamma (-\tau ),\forall \tau$ even

To recap the property about eh ${\gamma }_y(t_1,t_2)$ : the properties of a $SSP$ don’t depend on time $t$. In other words, what happens at time $t$ is representative also of what happens at time $t+\tau$ (no probabilistic difference).

White noise

A White Noise ($WN$) is a $SSP$ with $\gamma (\tau )=0$ for all $\tau \ne 0$.

A $WN$ is an unpredictable signal meaning that there is NO CORRELATION between $\eta (t_1)$ and $\eta (t_2)$. Usually, a $WN$ is defined as $\eta (t)\sim WN(0,{\lambda }^2)$. Having them with zero-mean is not mandatory.

The fact that the covariance function is zero everywhere except for the origin is another way to say that the past is not informative to know the future (whiteness property). We will use white noise to represent uncertainty in the model.

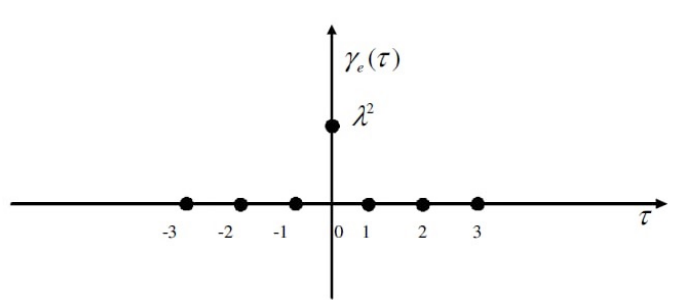
Unpredictable by definition.